梯形测试一下
A卷
1. 等腰梯形的腰长为5 ，上.下底的长分别为6 和12 ，则它的面积为_______.
2. 已知等腰梯形的底边长分别为2和8，高为4，则一腰长为______________________________
3. （1）顺次联结一个四边形四边的中点所得到的四边形是__________
（2）顺次联结一个平行四边形形四边的中点所得到的四边形是__________
4. 假如一个梯形的中位线长是6，高是5，那样它的面积是__________
5. 假如一个等腰梯形的中位线长10，腰长是4，那样它的周长是__________
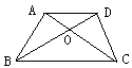
6. 如图，梯形ABCD中，对角线AC与BD交于点O，则图中面积相等的三角形有（ ）
A. 3对 B. 2对
C. 1对 D. 4对
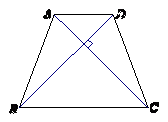
7. 任意四边形ABCD各边中点分别是E、F、G、H，若对角线AC、BD的长都为20cm，则四边形EFGH的周长是（ ）
A．80cm B．40cm C．20cm D．10cm
8. 给出下列四个命题
（1）顺次联结一个矩形四边的中点所得到的四边形是菱形
（2）顺次联结一个等腰梯形形四边的中点所得到的四边形是矩形
（3）顺次联结一个菱形四边的中点所得到的四边形是矩形
（4）顺次联结一个正方形形四边的中点所得到的四边形是正方形
其中正确的个数为（）
A. 1个B. 2个C. 3个D. 4个
9. 已知等腰梯形
中，
，对角线
，求梯形的高.
B卷
1. 假如等腰梯形两底之差等于一腰的长，那样这个等腰梯形的锐角等于__________
2. 一梯形上底为5，过上底一端引一腰的平行线与下底相交，若所得的三角形的周长为20，
则此梯形的周长为__________.
3. 在梯形ABCD中，AD∥BC，∠B=50°，∠C=80°，AD=8，BC=11，则CD=_______.
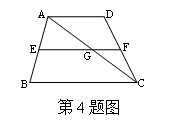
4. 如图，梯形ABCD中，AD∥BC，EF是梯形的中位线，对角线AC交EF于G，若BC=10cm，EF=8cm，则GF的长等于________________________________________cm．
5. 如图，菱形ABCD由6个腰长为2，且全等的等腰梯形镶嵌而成，则线段AC的长为__________
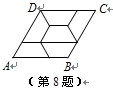
6. 假如一个梯形的上底与下底之比是1:5，那样这个梯形的中位线把梯形分成的两部分的面积比等于__________
7. 在梯形ABCD中，AD∥BC,∠B=90°，∠C=45°，CD=10 cm，BC=2AD，则梯形的面积为____ ___.
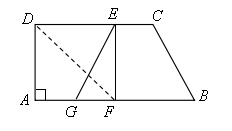
8. 如图，在直角梯形纸片中，
，
，
，将纸片沿过点
的直线折叠，使点
落在边
上的点
处，折痕为
．连接并展开纸片．
（1）求证：四边形
是正方形；
（2）取线段
的中点
，连接，假如，试说明四边形
是等腰梯形．
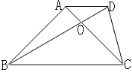
9．已知：如图，在梯形ABCD中，AD∥BC，AB=AC，∠BAC=90°，BD=BC，BD交AC于O.求证：CO=CD.
附加题
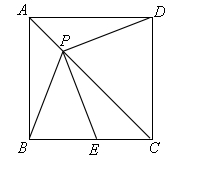
1．如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A.C不重合），点E在射线BC上，且PE＝PB.
（1）求证：① PE＝PD ； ② PE⊥PD；
（2）设AP＝x, △PBE的面积为y.求出y关于x的函数关系式，
并写出x的取值范围；
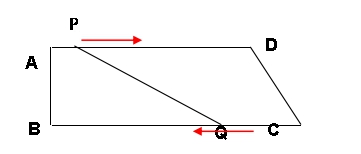
2．如图，在直角梯形ABCD中,AD//BC,∠B=900,AB=8cm,AD=24cm,BC=26cm,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动.点P、Q分别从点A.、C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.求:
.t为什么值时,四边形PQCD为平行四边形? 四边形PQCD为等腰梯形?
.t为什么值时,四边形ABQP为矩形?
